√ダウンロード 三角比の相互関係 タンジェント 797820

三角比 (サイン コサイン タンジェント) とは？定義と相互関係 ☭ 変換公式を思い出すためには、• tan（タンジェント）とは 最後にタンジェントはこうなります。 傾きを知る 「長さ」から「角度」 例えば、 影の長さから太陽の高度 角度 を測るのは、古くからある三角関数の利用方法の一つでした。タンジェントは、直線の傾き tanθ = y x tan θ = y x正接・正弦・余弦 直角三角形 ABC で、AB = c、 BC = a 、 CA = b とするとき 正接（tangent） 正弦（sine） 余弦（cosine） 余接、正割、余割 弧度法 半径 r の円で、長さ r の弧に対する中心角の大きさを単位として、角の大きさを測る方法を弧度法といい、この単位の大きさを1弧度（1ラジアン）をい

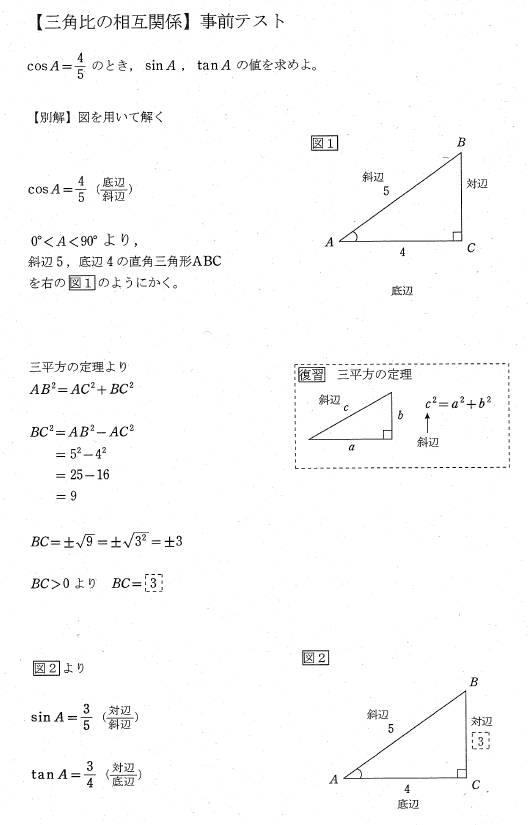
三角比の相互関係 事前テスト解答例 Kyokuryo Math

三角比の相互関係 タンジェント

三角比の相互関係 タンジェント-三角比 ①サイン、コサイン、タンジェント、三角比の表 教科書・プリント・問題集 48 図形と計量 鋭角の三角比 ②直角三角形の辺と角 ③三角比の相互関係 1つの三角比の値から他の三角比の値を求める 教科書・プリント・問題集 三角比の拡張、平面図形の計量 ①三角比と座標 三角比の座標に三角比の相互関係は、三角比の1つの値がわかれば、ほかの2つの値がわかる大事な公式です。 例題を解いてみましょう。 cosA＝3／4のとき、sinA まず、cosAからsinAの値を求めるには、三角比の相互関係のどの式を使うと良いか考えます。

Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau

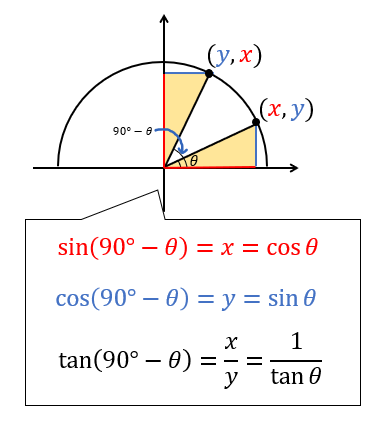
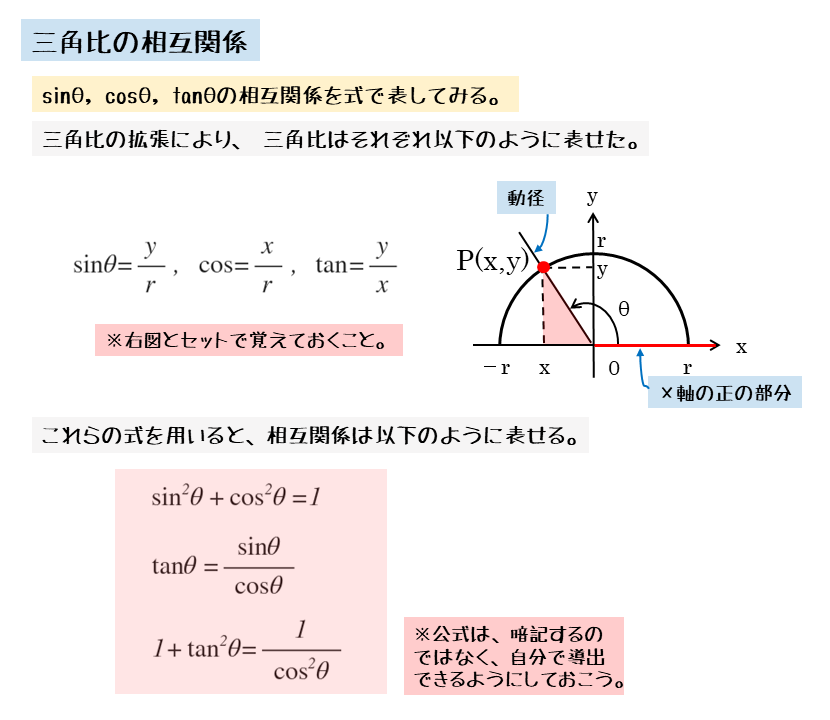
三角関数（三角比）の相互関係 関係式 sin 2 θ cos 2 θ = 1 ⇒ 証明 tan θ = sin θ cos θ （ただし， cos θ ≠ 0 ） ⇒ 証明 tan 2 θ 1 = 1 cos 2 θ （ただし， cos θ ≠ 0 ） ⇒ 証明 ここも参考にするとよい． 証明 1．三角関数の定義より（右図参照）， sin θ = y r ， cos θ = x r より，− 104 − 高校講座・学習メモ 数学Ⅰ 三角比の相互関係 ここで お約束事！ (sinθ)2 ≠sinθ2 ← ( )をそのまま外すのは 禁止！ (sinθ)2＝sin2θ と書き tan ⁡ ( 9 0 ∘ θ) = − 1 tan ⁡ θ \tan (90^ {\circ}\theta)=\dfrac {1} {\tan\theta} tan(90∘ θ) = −tanθ1 〜 18 0 ∘ − θ 180^ {\circ}\theta 180∘ − θ （補角）の公式〜 sin ⁡ ( 18 0 ∘ − θ) = sin ⁡ θ \sin (180^ {\circ}\theta)=\sin\theta sin(180∘ −θ) = sinθ cos ⁡ ( 18 0 ∘ − θ) = − cos ⁡ θ

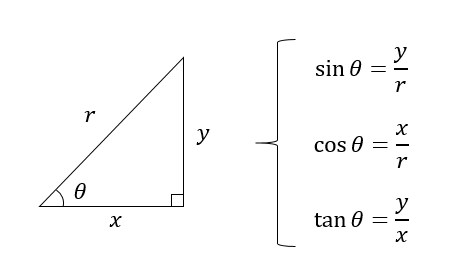
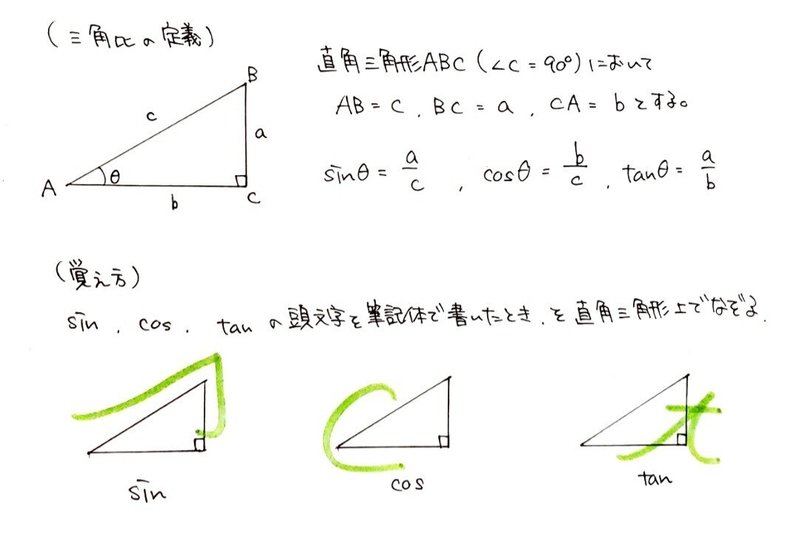
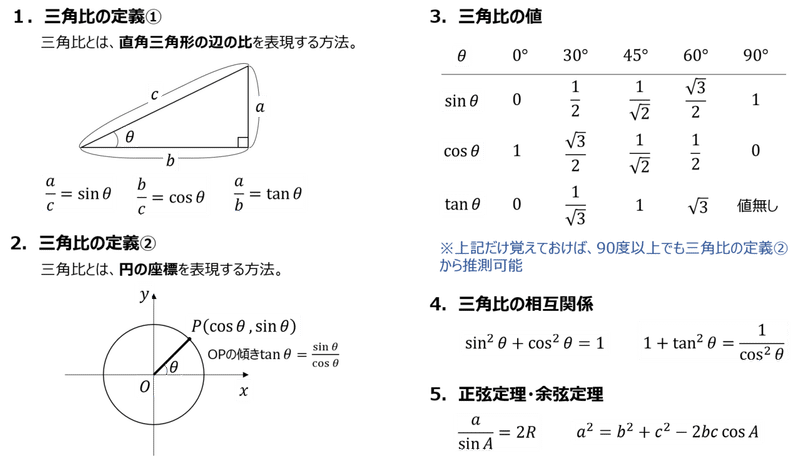
を角 𝜃 の またタンジェント(tangent) といい，tan𝜃 で表す。 また，比 AC AB, BC AB の値も様に三角形の大きさに関係なく， 角 𝜃 のみによって決まる。 比 AC AB を角 𝜃 の正弦またサイン(sine) といい，sin𝜃 で表す。 また，比 BC AB を角 𝜃 の余弦またサコイン(cosine) といい，cos𝜃 で表す。 B Aが現在地です． 高校数学Iで登場する「三角比の相互関係」とは、次の2つの公式のことです。 sin 2 A cos 2 A=1 (1) sin A cos Annnn (2) 三角比 sin A , cos A , tan A のうち1つ分かれば、残りはこれらの公式を使って「芋づる式に」求まります。 例えば、 sin A が このときの三角形の辺の２つの辺の比のことを 三角比 と言う。 ある1つの基準となる角度に対して、どの辺とどの辺を使った三角比なのかによって、サイン、コサイン、タンジェントと呼び方が変わってくる。

 サイン・コサイン・タンジェント a b c θ ∠acb=90°の直角三角形abcで∠abcが鋭角θで与えられた場合 辺の長さが変化しても abcは常に一定の形(相似)なので辺の比が定まる。 つまり、辺の比 ac ab 、 bc ab 、 ac bc はθの値によって決まる。 三角比 sinθ = ac ab ・・・正弦(サイン) cosθ = bc ab ・・・余弦 さて，三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$は独立したものではなく，互いに関係性をもっています． この三角比の間に成り立つ基本の関係式は $\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$ $\cos^{2}{\theta}\sin^{2}{\theta}=1$ $1\tan^{2}{\theta}=\dfrac{1}{\cos^{2}{\theta}}$三角比の相互関係を使って、次の問いに答えよ。ただし、$0^\circ\lt{A}\lt90^\circ$ である。 $\sin{A}=\dfrac{3}{5}$ のとき、$\cos{A}$、$\tan{A}$ の値を求めよ。 $\cos{A}=\dfrac{1}{3}$ のとき、$\sin{A}$、$\tan{A}$ の値を求めよ。 $\tan{A}=7$ のとき、$\cos{A}$、$\sin{A}$ の値を求めよ。 三角比の相互関係の利用の解答 $\sin^2A

三角関数 逆三角関数ほか 三角関数ファミリー を紹介 空間情報クラブ 株式会社インフォマティクス

わかりやすい三角比と基本公式 Irohabook

アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 角度と底辺から斜辺と高さを計算 直角三角形の底辺と傾斜角から斜辺と高さを計算します。 角度と高さから底辺と斜辺を計算 直角三角形の傾斜角と高さから底辺と斜辺を計算します。 角度と斜� 三角比 (サイン コサイン タンジェント) とは？ 定義と相互関係 21年2月19日 この記事では、「三角比」の定義や基本公式、そして計算問題をできるだけわかりやすく解説していきます。 （サイン コサイン タンジェント）とは何かについて、この記事を通して理解してくださいね！ 目次 非表示 三角比とは？ 三角比 sin cos tan の定義 三角比の定義の覚え方 タンジェントがわかれば、サインやコサインは計算で求められる。 そのためにあるのが、三角比の相互関係の公式です。 tanθ＝sinθ/cosθ sin2θ＋cos2θ＝1 1＋tan2θ＝1/cos2θ (2は指数として読んでください。 三角関数の倍角みたいに見えて嫌なんですけど

改訂版 ４プロセス数学 P71 ２ 三角比の相互関係

三角比の相互関係 事前テスト解答例 Kyokuryo Math

三角比の相互関係の 3 3 つめの式 tan2 θ 1 = 1 cos2θ tan 2 ⁡ θ 1 = 1 cos 2 ⁡ θ も利用できそうです。 これを式変形していくことで、解決することもできますが、 そもそも、 tan2 θ 1 =第1節三角比では、直角三角形の鋭角を定めたときの2辺の比を三角比とし て導入する。さらにそれらの相互関係に触れる。その後、鈍角への拡張となる。 そこでは、座標平面上で三角比が再定義される。続いて、再定義された三角比 の相互関係が導かれる。 三角比の相互関係① 上に示したように、三角比より と表すことができます。 これらの式を変形すると このように考えることができますね。 そして、直角三角形では三平方の定理が成り立つので 両辺を で割ると このように式を作ることができますね (^^) sinの2乗とcosの2乗を足した

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

三角比 三角関数 思考力を鍛える数学

Tanθって何を表す記号？ 今回から、本格的に 「三角比」 の学習が始まるよ。 最初に扱うのは、 「tanθ」 。 「tan」 は 「タンジェント」 と読むよ。 そして、 「θ」 は角度を表す記号で、 「シータ」 と読むよ。 ・・・と、紹介しておいて何だけど、この「tanθ」、すごく難しく見えないかな？ 数学なのに、いきなりよく 分からない英語 が出てくるし、 見慣れ①三角比の相互関係導入時 （5）指導上の留意点 新出事項とその特徴が多数の意見に埋没しないようにすること 9 授業展開例 （45 分授業の場合） 時間(分) 指導内容 (下線部は生徒に答えを問う) 指導上の留意点 導入 (10) 三角比の学 習意義と値 の求め方の 確認 ・始めに三角比とは三角比は数学 Ⅰで扱われ，三角関数は数学Ⅱで扱うのもここ 年間変わらない。これでよいのだろうか？ 三角比はまったくの図形的な扱いに終始し，三 角関数は，代数的な式計算や関数の扱いにな る。よもや数学Ⅰでやった三角比がこのような

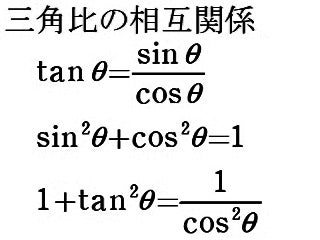
三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

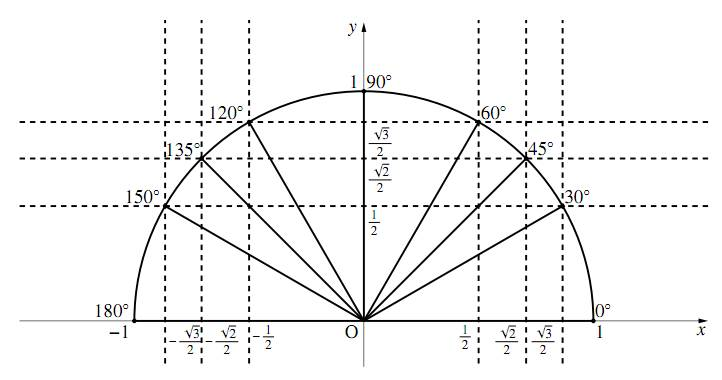
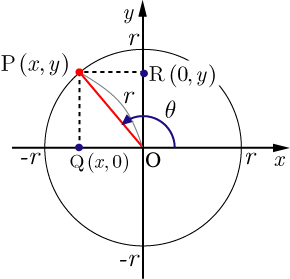
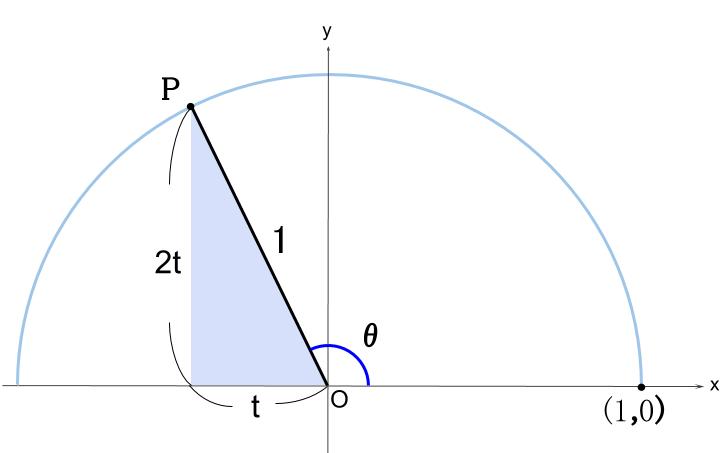
 三角比・三角関数の定義 三角比については、以下の記事で詳しく説明しています。 三角比 (サイン コサイン タンジェント) とは？定義と相互関係 三角比・三角関数の代表的な値は頭に定着させておきましょう！ 三角比の相互関係 半径1の円（単位円）を考えます。 O(0,0) O (0, 0), A(1,0) A (1, 0) とし、半円（上半分）の円周上に、 ∠POA = θ ∠ P O A = θ となる点 P をとります。 このとき、 P(x,y) P (x, y) とすると、 cosθ = x cos 今までの3つの公式に加えて，以下の公式も三角関数の相互関係と呼ばれることがあります： 1 1 tan ⁡ 2 θ = 1 sin ⁡ 2 θ 1\dfrac{1}{\tan^2\theta}=\dfrac{1}{\sin^2\theta} 1 tan 2 θ 1 = sin 2 θ 1

3

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

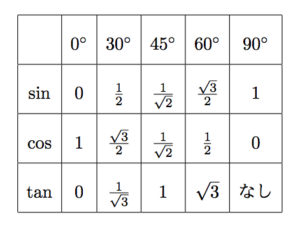
1 tan2 = 1 cos2 3個目の1 tan2 = 1 cos2 は、1個目、2個目のsin2 cos2 = 1;三角比 1 タンジェント 8 0 ,90 ,180 の三角比 2 サイン 9 相互関係 3 コサイン 10 三角形の面積 4 相互関係（鋭角） 11 正弦定理 5 鈍角の三角比 12 正弦定理と外接円 6 相互関係（鈍角） 13 余弦定理1 7 性質 14 余弦定理2Tan = sin cos ;

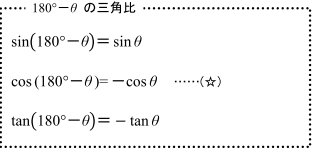
180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座

高1数学a 三角比の相互関係 なぜマイナスをつけるのかがわかりません 高校 教えて Goo

現在地 と前後の項目 高校数学Iで登場する「三角比の相互関係」とは、次の2つの公式のことです。 sin 2 Acos 2 A=1 (1) sinAcosAnnnn (2) 三角比 sinA , cosA , tanA のうち1つ分かれば、残りはこれらの公式を使って「芋づる式に」求まります。 例えば、 sinA が本日のお題 次の問いを通して，三角比の相互関係を考えます 1 次の問いに答えましょう (1) 0° ≦ θ ≦ 180° で sinθ = 3 5 を満たすとき， cosθ と tanθ の値は？ (2) θ が第2象限の角で tanθ = − 2 を満たすとき， sinθ と cosθ の値は？ 2 0° ≦ θ ≦ 180° で定義さTan = sin cos で sin を消去したものです。簡単ですが、一応導いてお

高校数学 三角比 使って覚える三角比の基本公式 数学の面白いこと 役に立つことをまとめたサイト

三角比の相互関係の公式４つって 証明 覚え方 応用問題６選を解説 遊ぶ数学

まずは解法1、三角関数の相互関係を使って求めていきます。三角形の相互関係とは以 下の通りです。 三角関数の相互関係 sin2 cos2 = 1;

Tan A A Ainadfrac34 Cosa Descubre Como Resolverlo En Qanda

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

3分で分かる 三角関数の基礎知識 合格サプリ

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

3

数学 三角比 Sin Cos Tanの相互関係と覚え方 理系ラボ

大学受験で使う数学を一から始めるひとのための三角比基礎の勉強法

三角関数 Wikipedia

高校数学 数 ７６ 三角比 基本編 Youtube

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

1

三角比の相互関係 公式３つの覚え方と使い方は 数スタ

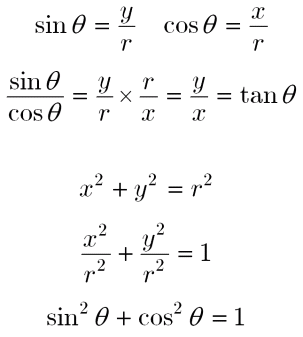
三角比 三角関数の相互関係と 象限 大人が学び直す数学

三角比１５ 相互関係の指導の最適化 怜悧玲瓏 高校数学を天空から俯瞰する

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

タンジェントとは何か 中学生でも分かる三角関数の基礎

三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

基本 三角関数の相互関係 なかけんの数学ノート

三角比の相互関係 思考力を鍛える数学

三角比の拡張 数学i フリー教材開発コミュニティ Ftext

高校数学 三角関数の相互関係を用いる証明 練習編 映像授業のtry It トライイット

高校数学無料問題集 数 第３章 図形と計量 三角比の拡張と相互関係の式 桝 ます Note

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 21年3月16日 エキサイトニュース 4 7

単位円を導入したら即座に触れたいこと 怜悧玲瓏 高校数学を天空から俯瞰する

図形と計量 三角比の相互関係について その１ 日々是鍛錬 ひびこれたんれん

三角比公式 高中三角比公式 Pbhcl

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

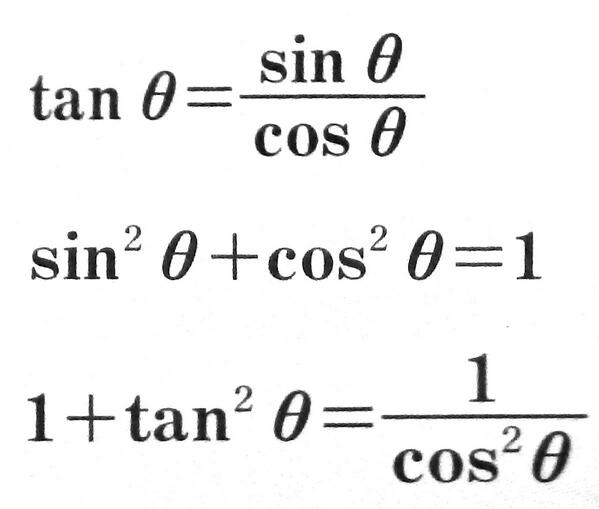
画像でわかる高校数学bot V Tvittere 三角比 三角比の相互関係 T Co Oerqbx2bmb

Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau

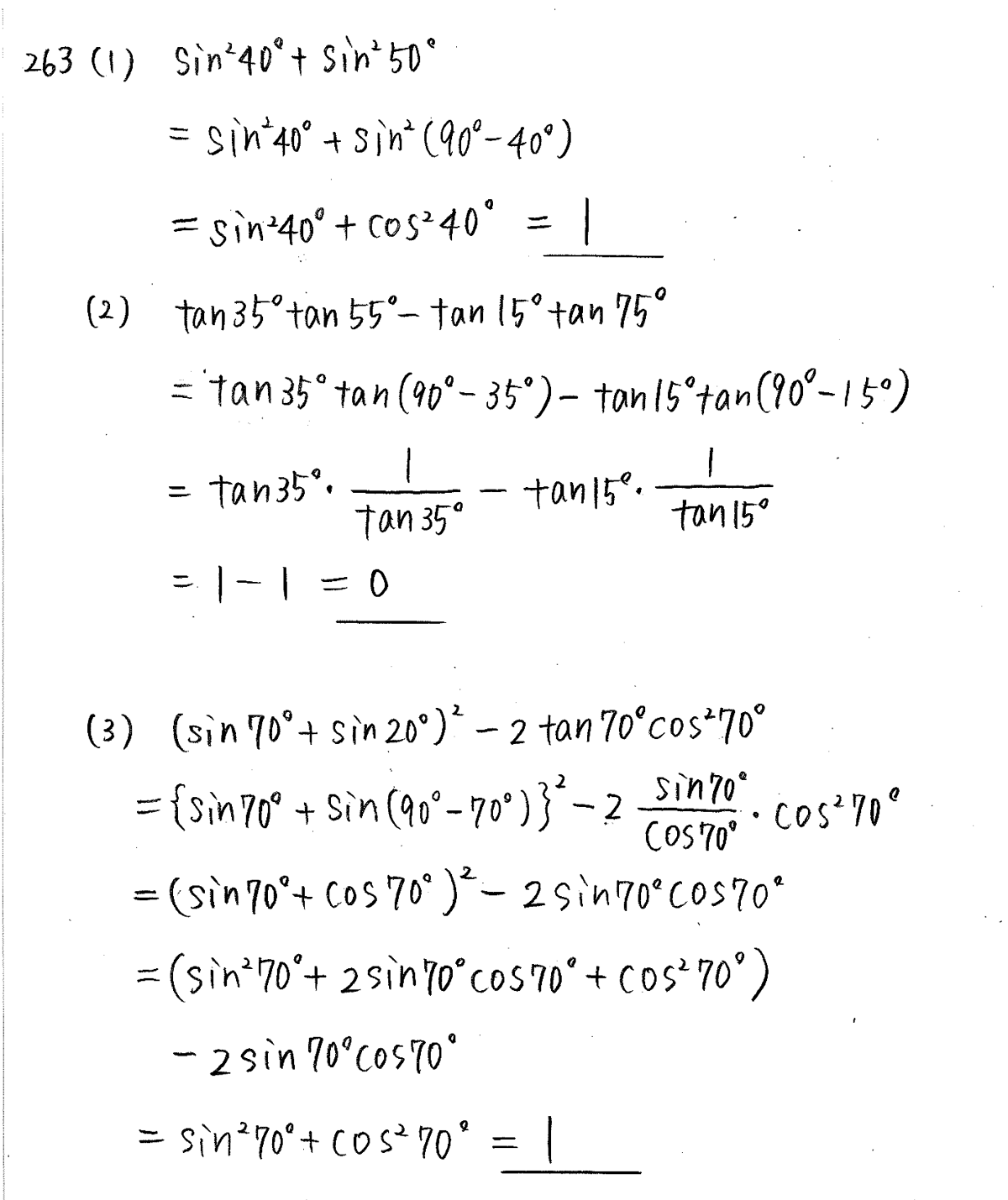
クリアー数学 数1 P64 23 三角比の相互関係

26 三角比の相互関係 正接の解き方と 27 Clear

Studydoctor三角比の相互関係と計算 高校数学 Studydoctor

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

三角関数とは コトバンク

数学 三角比 Sin Cos Tanの変換公式と覚え方 理系ラボ

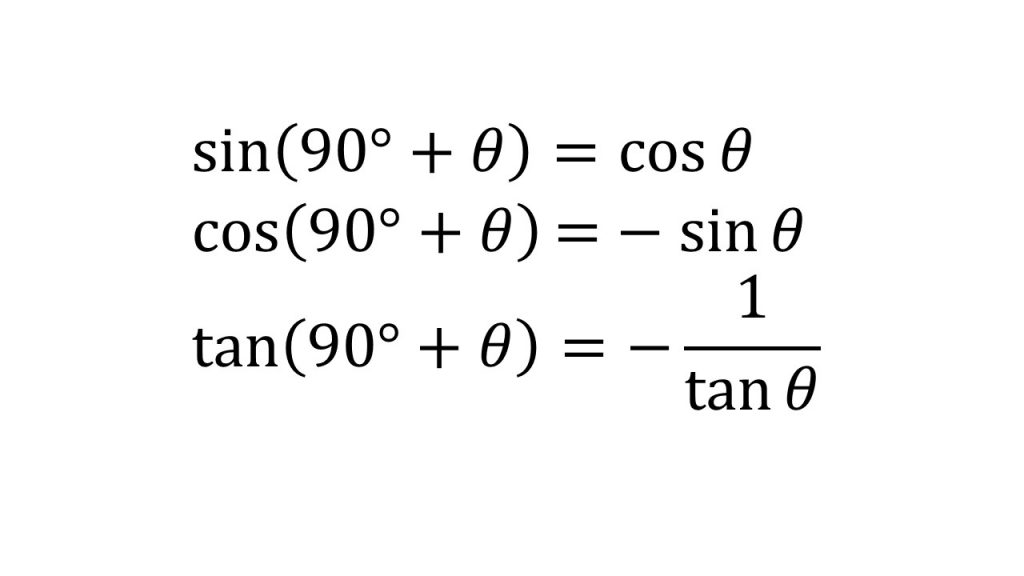
三角比公式 大学受験の王道

高校数学 数 ７７ 三角比 公式編 Youtube

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説

高校数学 三角関数の2倍角の公式 半角の公式の証明と応用 受験の月

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

数学ia 三角比の相互関係 大学入試数学の考え方と解法

三角関数の相互関係

三角関数 Wikipedia

48s96ub7b0z5f Net Sankakuhi Sougo

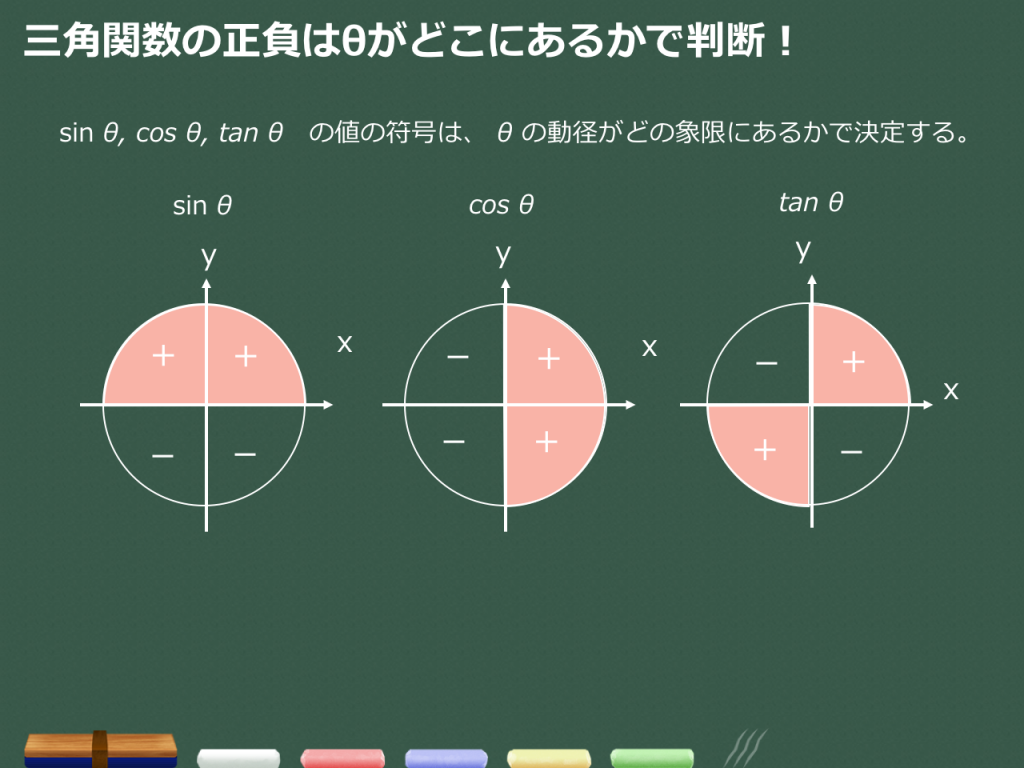
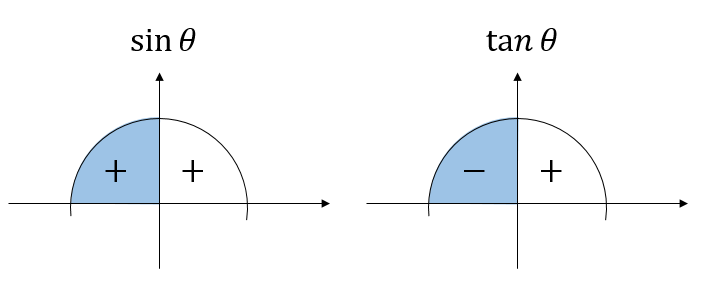
三角関数の値の正負 数学ii By Okボーイ マナペディア

三角比の相互関係の問題について解説お願いします Tan8 3 Yahoo 知恵袋

この公式は 直角三角形の時以外も使えるのでしょうか Clear

高校数学 連立三角方程式 三角関数の相互関係 合成 加法定理の利用 受験の月

数学 三角関数 三角関数の相互関係 オンライン無料塾 ターンナップ

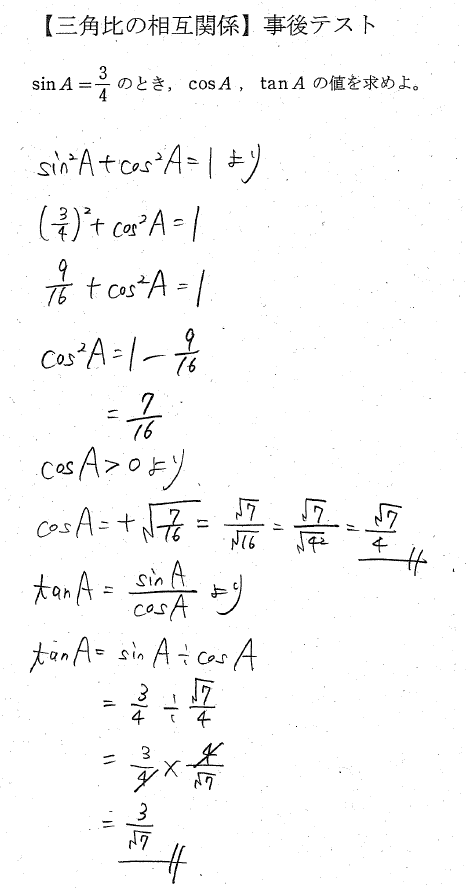
三角比の相互関係 事後テスト解答例 Kyokuryo Math

三角比の相互関係の3つの公式の使い分けの見極め方を教えていただきたい Yahoo 知恵袋

三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

図形と計量 三角比の相互関係について その１ 日々是鍛錬 ひびこれたんれん

三角比の相互関係 事前テスト解答例 Kyokuryo Math

基本 三角関数の相互関係 なかけんの数学ノート

高校数学 A 三角比の相互関係level2 0 8 180 でcosからsin Tanを求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

三角関数 の基本的な定理とその有用性を再確認してみませんか その２ 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所

公式証明道場２ 三角比の相互関係 数学 Aで学びたい高校のnote塾 Note

三角比の相互関係とその使い方 高校数学の知識庫

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

三角比の相互関係 鈍角の場合 高校数学の無料オンライン学習サイトko Su

数学 三角比 Sin Cos Tanの相互関係と覚え方 理系ラボ

三角比の相互関係 公式３つの覚え方と使い方は 数スタ

高校数学 A 三角比 三角比の相互関係 Sin Cos Tanの三角関係 やはり俺の考察ブログはまちがっている アニメ 数学

48s96ub7b0z5f Net Sankakukansuu Koushiki

三角比は1時間で解けるようになる 箕輪 旭 Note

基本 三角比の相互関係 なかけんの数学ノート

三角比 入門編 Sin Cos Tanって何 90 8 の公式も ますますmathが好きになる 魔法の数学ノート

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

1枚目の写真が三角比の相互関係で298 300の問題 Clear

三角比を用いた計算問題をマスターしよう スタディクラブ情報局

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

サインコサインタンジェント Sin Cos Tan とは何を表す 良い覚え方を紹介 遊ぶ数学

三角比の相互関係とその使い方 高校数学の知識庫

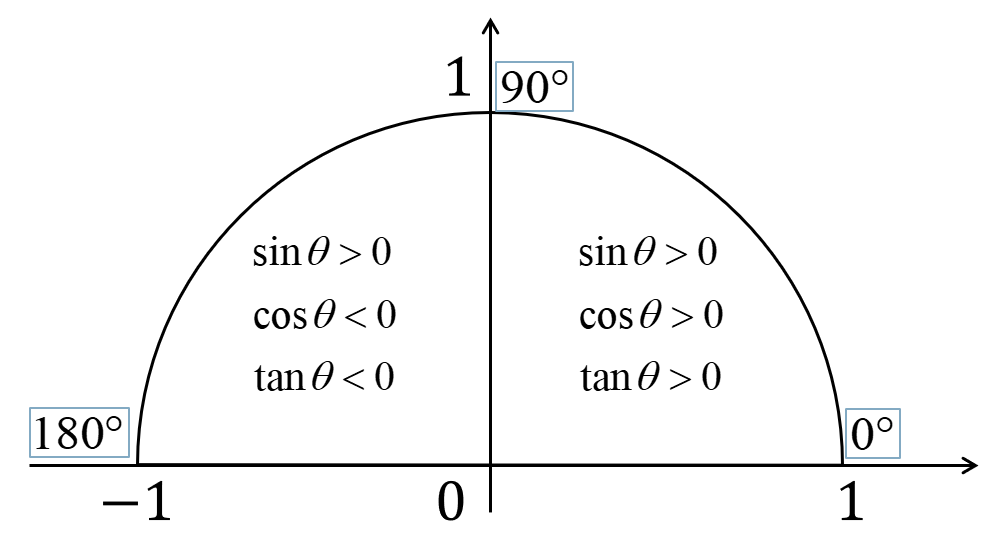
数学 鈍角での三角比の相互関係の公式の使い方とコツ ページ 2 教科書より詳しい高校数学

高校数学 A 三角比の相互関係level2 0 8 180 でcosからsin Tanを求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

Tanの値からcosの値を求めるときの分数の式変形について 数学 苦手解決q A 進研ゼミ高校講座

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

高1 数1 三角比 高校生 数学のノート Clear

三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

三角関数の相互関係 短時間座標計算法

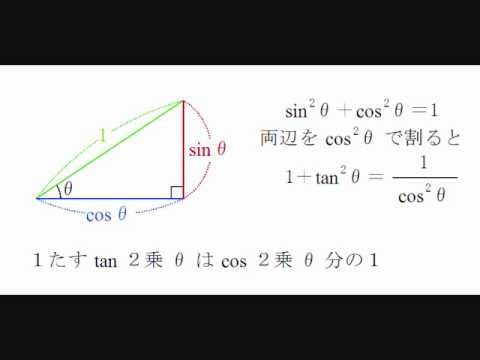
歌って覚える三角比 ２ 三角比の相互関係 Youtube

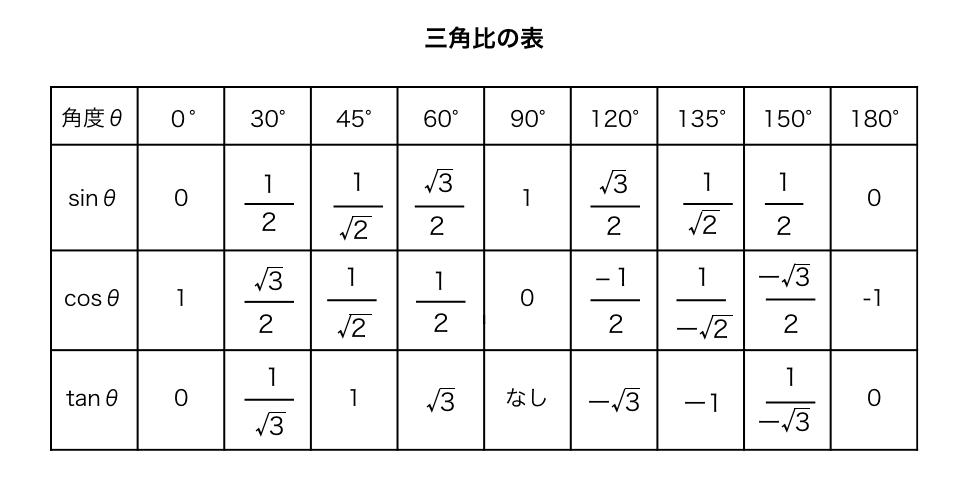
三角関数の公式 Sin Cos Tan と覚え方

高校数学 90 8の三角比 映像授業のtry It トライイット